AN ASYMMETRY COEFFICIENT FOR MULTIVARIATE DISTRIBUTIONS

© Michel Petitjean (retired since Jan 1st, 2023)

Author's professional address:
INSERM ERL U1133 (BFA, CNRS UMR 8251), Université Paris Cité
35 rue Hélène Brion, 75205 Paris Cedex 13, France.

Formerly (2010-2018): MTi, INSERM UMR-S 973, Université Paris 7.
Formerly (2007-2009): CEA/DSV/iBiTec-S/SB2SM (CNRS URA 2096), Saclay, France.
Formerly (1987-2006): ITODYS, CNRS UMR 7086, Université Paris 7.

Contact: petitjean.chiral@gmail.com



Related topics:


The skewness m3 of an univariate distribution is the centered third-order moment normalized to the cube of the standard deviation. The square of the skewness, M3, was introduced by Pearson in 1895 (see ref. [1], p. 351) to measure the degree of asymmetry of a distribution. The squared skewness has an upper bound: M3 ≤ m4 - 1, where m4 is the kurtosis of the distribution, i.e. the centered fourth-order moment normalized to the square of the variance. This inequality is a consequence of a more general one standing for multivariate distributions (see eq. 6 in [2]). Many asymmetry coefficients were proposed in the statistical literature (see section 4.2 in [3] for an historical survey). The centered third-order moment and its multivariate analogs vanish for a symmetric distribution, although there are non-symmetric distributions with a null third-order moment (this is the case of the asymmetric distribution such that Prob(-4)=1/3, Prob(1)=1/2 and Prob(5)=1/6, as noticed in ref. [4]). It should be noticed here that the term "symmetry" denotes in this context an indirect symmetry (chirality) rather a direct symmetry (this latter is undefined in the univariate case).
Despite its major drawback, the third-order moment has been widely used, probably due to its simplicity and to the fact that most known asymmetry coefficients offer the same drawback.

The chiral index is an asymmetry coefficient which is null IF and ONLY IF the distribution is symmetric (i.e. achiral).
In the univariate case, the chiral index is expressed from the lower bound Rmin of the correlation coefficient between the distribution and itself:

CHI = ( 1 + Rmin ) / 2

The mean m and the variance s2 are assumed to exist. CHI takes values in [0;1/2] because Rmin cannot be positive.
As a consequence of the convergence theorem in [5], the chiral index of a sample of n observations of a random vector in Rd converges to the chiral index of its parent distribution.
The chiral index CHI of a set of n observations xi (i=1..n), sorted in increasing order is calculated like this:

2 CHI - 1 = Rmin = [ (x1-m)(xn-m) + (x2-m)(xn-1-m) + ... + (xn-1-m)(x2-m) + (xn-m)(x1-m)  ] / ns2

CHI is thus easily computable with a pocket calculator: (a) sort the set with increasing values and then with decreasing values, (b) compute the correlation coefficients between the sorted sets, (c) add 1 and then divide by 2. Note that the correlation coefficient cannot be positive.

CHI may be expressed with the squared midranges or with the squared range lengths: (see equations 2.9.4 and 2.9.5 in [3])

CHI can be used for symmetry testing: tables of quantiles of the sampling distribution were published, under assumption of uniformity and of normality [6].

The chiral index is defined for multivariate distributions. It is derived from a probability metric and has formal relations with the Monge-Kantorovitch transportation problem: see The Mathematical Theory of Chirality.


SOME MAXIMALLY CHIRAL DISTRIBUTIONS


The upper bound of the chiral index is 1/2 for univariate distributions.
This bound is asymptotically reached for the Bernouilli distribution when its parameter tends to 0 or to 1 [5].

When d=2, the upper bound of the chiral index is shown [7] to lie in the interval [1-1/π;1-1/2π].
The bound 1-1/π is conjectured to be optimal and it is asymptotically reached for a rather awkward family of bivariate distributions [7].
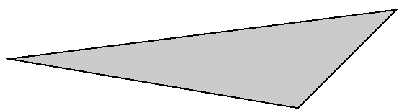
The most chiral triangle, i.e. the most chiral three points set, is known [8]: see Fig. 1.

For d=3, the most chiral tetrahedron, i.e. the most chiral four points set, is unknown.
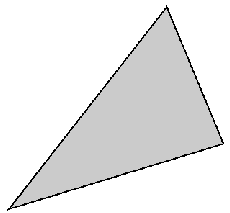
However the most chiral disphenoid (or isosceles tetrahedron, or equifacial tetrahedron), is known [9].
Its chiral index and its triangular face are given in Fig. 2.

For any d value, the upper bound of the chiral index is shown [10] to lie in the interval [1/2;1].
The upper bound of the chiral index of a d-variate distribution remains unknown when d>1.
A summary of several known extreme distributions ia available in [11].

Fig. 1. The most chiral triangle: CHI = 1-2(51/2)/5
Squared lengths ratios: 1:(5+151/2)/2:(4+151/2)
Coordinates: see ref [7].

Fig. 2. The triangular face of the most chiral disphenoid: CHI = 3(13-6(21/2))/97
Squared lengths ratios: 1:3-21/2/2:3
Coordinates: see ref [8].



REFERENCES


  1. PEARSON K.
    Contributions to the Mathematical Theory of Evolution,-II. Skew Variation in Homogeneous Material.
    Phil. Trans. Roy. Soc. London (A.) 1895, 186, 343-414.

  2. PETITJEAN M.
    The Chiral Index: Applications to Multivariate Distributions and to 3D molecular graphs.
    Proceedings of 12th International Symposium on Operations Research in Slovenia, SOR'13, pp. 11-16,
    Dolenjske Toplice, Slovenia, 25-27 September 2013.
    L. Zadnik Stirn, J. Zerovnik, J. Povh, S. Drobne, A. Lisec, Eds.
    Slovenian Society Informatika (SDI), Section for Operations Research (SOR), Ljubljana, 2013.
    (the full book of the proceedings is available in open access, ISBN 978-961-6165-40-2)
    Download pdf paper from the HAL repository: hal-01952400
    (deposited with permission from Society Informatika, Section for Operations Research)
    Download PDF file of the lecture.

  3. PETITJEAN M.
    Chirality and Symmetry Measures: A Transdisciplinary Review.
    Entropy 2003, 5[3], 271-312 (open access paper: DOI 10.3390/e5030271; Zbl 1078.00503).

  4. ĐORIĆ D., NIKOLIĆ-ĐORIC E, JEVREMOVIĆ V, MALIŠIĆ J.
    On measuring skewness and kurtosis.
    Qual. Quant. 2009, 43, 481-493 (DOI 10.1007/s11135-007-9128-9).

  5. PETITJEAN M.
    Chiral Mixtures.
    J. Math. Phys. 2002, 43[8], 4147-4157 (DOI 10.1063/1.1484559).
    A free copy for personal use only (©AIP, American Institute of Physics) is available from the HAL repository: hal-02122882; copyright rules apply.

  6. PETITJEAN M.
    Tables of Quantiles of the Distribution of the Empirical Chiral Index in the Case of the Uniform Law and in the Case of the Normal Law.
    arXiv:2005.09960 [stat.ME], 2020.

  7. COPPERSMITH D., PETITJEAN M.
    About the Optimal Density Associated to the Chiral Index of a Sample from a Bivariate Distribution.
    Compt. Rend. Acad. Sci. Paris, série I, 2005, 340[8], 599-604 (DOI 10.1016/j.crma.2005.03.011).

  8. PETITJEAN M.
    About Second Kind Continuous Chirality Measures. 1. Planar Sets.
    J. Math. Chem. 1997, 22[2-4], 185-201 (DOI 10.1023/A:1019132116175).
    Free version for readers: https://rdcu.be/bzS0P (link created by ; downloads, prints and copies are for subscribers only)

  9. PETITJEAN M.
    The Most Chiral Disphenoid.
    MATCH Commun. Math. Comput. Chem., 2015, 73[2], 375-384.

  10. PETITJEAN M.
    About the Upper Bound of the Chiral Index of Multivariate Distributions.
    AIP Conf. Proc. 2008, 1073, 61-66 (DOI 10.1063/1.3039023).
    A free copy for personal use only (©AIP, American Institute of Physics) is available from the HAL repository: hal-01954470; copyright rules apply.

  11. PETITJEAN M.
    Extreme asymmetry and chirality. A challenging quantification.
    Symmetry: Culture and Science 2020, 31[4], 439-447.
    Download PDF paper from the HAL repository: hal-03033327 (copy deposited with permission from Symmetrion).